Một thợ in về hưu tìm ra hình "einstein", giải thành công bài toán nổi tiếng

Ban đầu, nỗ lực giải bài toán einstein chỉ đơn giản là tìm cách trả lời câu hỏi: liệu có một tập hợp hình nào có thể được ghép lại để phủ lên một mặt phẳng mà không tạo ra chu kì? Nhưng các nhà khoa học tối giản đáp án theo thời gian.

Tháng Mười một vừa qua, David Smith gặt hái thành công sau một thập kỷ nỗ lực. Tự xưng là một cá nhân đam mê hình học, người đàn ông Anh Quốc cho rằng mình đã tìm ra lời giải cho bài toán ghép hình trong Toán học: ông khẳng định mình đã được một “einstein” và đứng tên xuất bản nghiên cứu để chứng minh điều đó.

Thuật ngữ einstein chỉ một mảnh ghép đơn phi chu kỳ - là một hình hài có thể ghép khớp được với nhau trên một mặt phẳng, đồng thời ghép vào thành một mẫu hình vô tận không lặp lại. Danh từ “einstein” ghép từ hai từ tiếng Đức, “ein” nghĩa là “một” và “stein” nghĩa là “đá”; có thể hiểu nôm na “einstein” tức là “một phiến đá”.

Những mẫu hình bạn thường thấy - như sàn gạch hay giấy dán tường - có thể tạo thành một hình ghép tới vô tận và lặp lại theo chu kỳ. Một einstein không tuân theo quy luật đó, và đã từ lâu các nhà toán học đi tìm một hình hài duy nhất có thể phủ kín một mặt phẳng theo một cách phi chu kỳ như thế. Vấn đề hóc búa này được đặt tên là “bài toán einstein”, và có vinh dự “cùng họ” với nhà vật lý học lỗi lạc Albert Einstein.

 “Tôi luôn thích thú mày mò và thử nghiệm với hình dáng”, ông Smith, thợ in về hưu nay đã 64 tuổi, thổ lộ trên trang WordPress cá nhân. Ông hứng thú với toán học thuở còn ngồi trên ghế nhà trường mà không thực sự xuất sắc trong môn học cổ đại. Nhưng đã từ lâu, ông Smith đam mê tìm lời giải cho bài toán einstein.

Kết luận trong báo cáo khoa học mới được đăng tải bởi chính ông Smith và ba chuyên gia toán học và điện toán khác khẳng định bài toán đã có đáp án. Các nhà nghiên cứu gọi einstein do ông David Smith tìm ra là “cái mũ”, bởi lẽ nó có mang dáng dấp của một chiếc mũ phớt. Ở thời điểm công bố được nhắc tới trên tạp chí The New York Times, báo cáo khoa học của nhóm chuyên gia chưa được hội đồng có chuyên môn thẩm định.

 “Đây có vẻ là một khám phá đáng ghi nhận!”, Joshua Socolar, nhà vật lý học công tác tại Đại học Duke trả lời trong một email, bộc lộ cảm xúc phấn khởi khi đọc một phiên bản chưa hoàn thiện của báo cáo nói trên. “Khía cạnh đáng chú ý nhất với tôi là [những hình ghép] không giống với bất cứ cấu trúc quen thuộc nào mà ta biết”.

“Kết quả bài toán gợi ra những câu hỏi thú vị liên quan tới vật lý”, ông Socolar nói thêm. Vị chuyên gia nhận định một người có thể bắt gặp cấu trúc này trong tự nhiên, hay thiết kế một cấu trúc dạng này để phục vụ những mục đích nhất định.

Ban đầu, nỗ lực giải bài toán einstein chỉ đơn giản là tìm cách trả lời câu hỏi: liệu có một tập hợp hình nào có thể được ghép lại để phủ lên một mặt phẳng mà không tạo ra chu kỳ?

Năm 1961, nhà toán học Hao Wang công bố báo cáo khẳng định một tập hợp như vậy là bất khả thi. Nhưng không lâu sau, học trò của ông Wang, ông Robert Berger đã sớm phủ nhận ước đoán này của người thầy. Giáo sư Berger khám phá ra một tập hợp hình học phi chu kỳ ghép lại từ 20.426 hình đơn lẻ, và không lâu sau đó ông Berger tiếp tục phát hiện ra một tập hợp khác ghép từ 104 hình.

Và cách giải bài toán einstein thay đổi: vẫn đi tìm cách phủ mặt phẳng, nhưng giờ các nhà toán học tìm cách tạo ra einstein với ít số hình nhỏ nhất có thể. Thập niên 70, Ngài Roger Penrose - nhà vật lý toán học công tác tại Đại học Oxford, cha đẻ của tam giác Penrose trứ danh, người đoạt giải Nobel vật lý 2020 nhờ đóng góp trong nghiên cứu lỗ đen  - giảm số hình ghép thành einstein xuống con số 2.

Sau Penrose, đã có những chuyên gia khác tìm được cặp hình của riêng mình. “Tôi cũng có một cặp hình như vậy”, Chaim Goodman-Strauss, nhà toán học công tác tại Bảo tàng Toán học Quốc gia ở New York, và cũng đồng tác giả báo cáo khoa học mới đăng tải, nhận định.

Ông nói thêm, bên cạnh mẫu bàn cờ vua quen thuộc, những hình vuông với hai màu đen trắng cũng có thể được ghép lại và tạo ra những mẫu hình phi chu kỳ. “Việc tạo nên những mẫu hình kỳ lạ và thú vị có thể coi là bình thường”, giáo sư Goodman-Strauss nói. Đó là lý do khiến hai mảnh ghép hình Penrose - vốn CHỈ có thể tạo ra những mẫu hình phi chu kỳ khi ghép - lại phi thường đến vậy.

Với ước mơ tối giản vấn đề toán học phức tạp, đã từ lâu các nhà nghiên cứu kiếm tìm một mảnh ghép duy nhất có khả năng tạo thành một mẫu hình bất tận trên một mặt phẳng, đồng thời không lặp lại theo một chu kỳ nhất định. Ngài Roger Penrose tạm gác lại hành trình tìm mảnh ghép độc nhất đã vài năm, nhưng đam mê khám phá vẫn hiện rõ nơi ông.

“Tôi đã đưa con số mảnh ghép xuống tới hai, và giờ ta đã đưa nó xuống còn một mảnh duy nhất!”, Ngài Penrose hồ hởi trước phát hiện cái mũ của ông Smith. “Tôi không có lý do gì để không đặt niềm tin vào nó”, nhà toán học người Anh nói thêm.

Báo cáo khoa học của ông Smith chứa hai cách chứng minh, đều được thực hiện bởi đồng tác giả, lập trình viên phần mềm Joseph Myers. Một bằng chứng dựa trên những lập luận truyền thống kết hợp một đoạn code do lập trình viên người Anh thảo nên; bằng chứng còn lại do giáo sư Myers soạn thảo mà không cần tới sự trợ giúp của máy tính.

Ngài Roger nói số bằng chứng được mô tả trong báo cáo “rất phức tạp”, khiến ông “tò mò vô cùng”. Ngài đồng thời nhận định, hình do ông Smith luận ra đơn giản một cách đáng ngạc nhiên.

Sự đơn giản tới một cách thân thành. Ông Smith cố gắng giải bài toán einstein bằng tay: ban đầu, ông Smith “táy máy” với phần mềm giải đố PolyForm do lập trình viên Jaap Scherphuis viết nên. Khi hình hài trên màn hình có tiềm năng trở thành lời giải cho bài toán einstein, ông Smith sẽ dùng máy cắt tạo ra những miếng ghép thực tế, cố gắng ghép chúng với nhau như một câu đố xếp hình kỳ lạ.

“Cảm giác [cầm miếng ghép hình trên tay] luôn hấp dẫn”, ông Smith mô tả việc ghép hình, xoay hình theo bất cứ cách nào mình muốn. “Việc này cũng khiến tôi chìm trong dòng suy nghĩ. Và nó giúp tôi hiểu hơn về cách một hình dáng lát sao cho hợp lý lên một mặt phẳng”.

Hồi tháng Mười một, khi Smith tìm ra một hình hài có thể phủ kín một mặt phẳng mà không tạo ra mẫu hình lặp lại, ông lập tức email cho Craig Kaplan, một nhà khoa học máy tính công tác tại Đại học Waterloo.

“Liệu hình này có phải câu trả lời cho ‘bài toán einstein’”, ông Smith đặt câu hỏi trong email. Tiến sĩ Kaplan sử dụng thuật toán của mình - được xây dựng dựa trên những nghiên cứu tương tự - để tạo ra một mặt phẳng lớn ghép từ những cái mũ. “Có vẻ mặt phẳng [ghép từ những cái mũ] do phần mềm tạo ra không có giới hạn”, ông Kaplap cho hay.

Dựa trên những dữ liệu thô này, ông Smith và Tiến sĩ Kaplan dùng … mắt thường để tiếp tục nghiên cứu trật tự của cấu trúc ghép từ những chiếc mũ. Áp dụng chứng minh phi chu kỳ truyền thống - một chứng minh toán học “được lôi ra khỏi ngăn kéo mỗi khi bạn có một bộ mẫu hình ghép phi chu kỳ”, hai nhà nghiên cứu phát hiện ra hình ghép từ cái mũ thỏa mãn những gì chứng minh nêu ra.

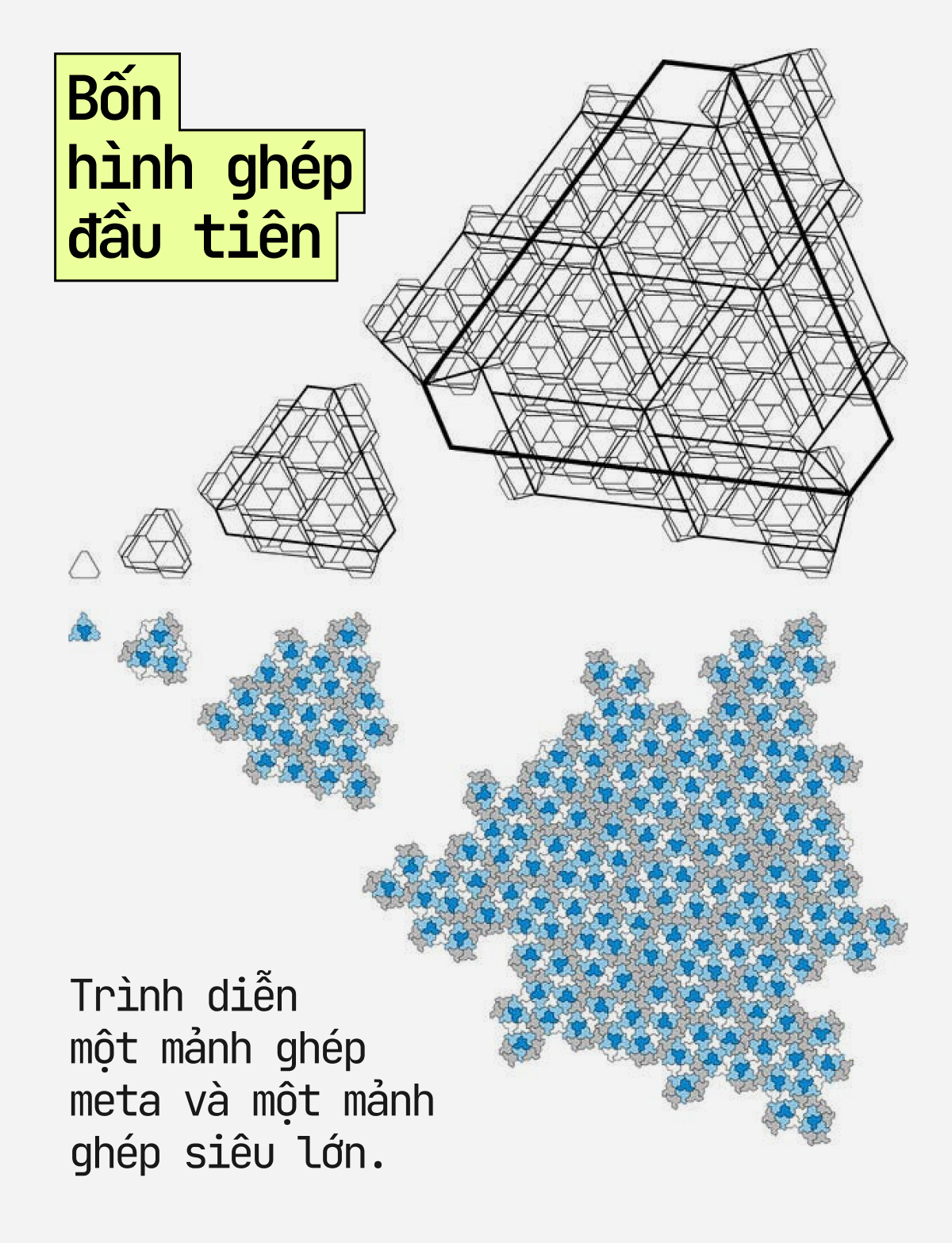
Theo lời Tiến sĩ Kaplan, đầu tiên phải xác định được một mảnh ghép meta - một hình đơn giản có thể đại diện cho một nhóm bao gồm một, hai hoặc bốn chiếc mũ. Khi ráp lại, các mảnh ghép meta này sẽ tạo thành một hình lớn hơn nhưng vẫn có những đặc tính tương tự. Cứ ghép những mảnh meta này từ nhỏ tới lớn, từ lớn tới siêu lớn và siêu siêu lớn, cho tới vô tận, và rồi ta sẽ có “một ‘sàn’ toán học lớn phủ đầy những bản thể của cái mũ”, Tiến sĩ Kaplan cho hay.

Đường link này có thể dẫn bạn tới một trang web giúp bạn tự ghép cho mình một einstein tạo thành từ những cái mũ.

Tiến sĩ Kaplan làm rõ, rằng hình chiếc mũ không phải là một khái niệm mới trong hình học. Thực tế nó là một hình đa giác được ghép từ các hình “kite” - hình “diều”, là một tứ giác với hai cặp cạnh liền kề bằng nhau, đối xứng nhau qua một đường chéo.

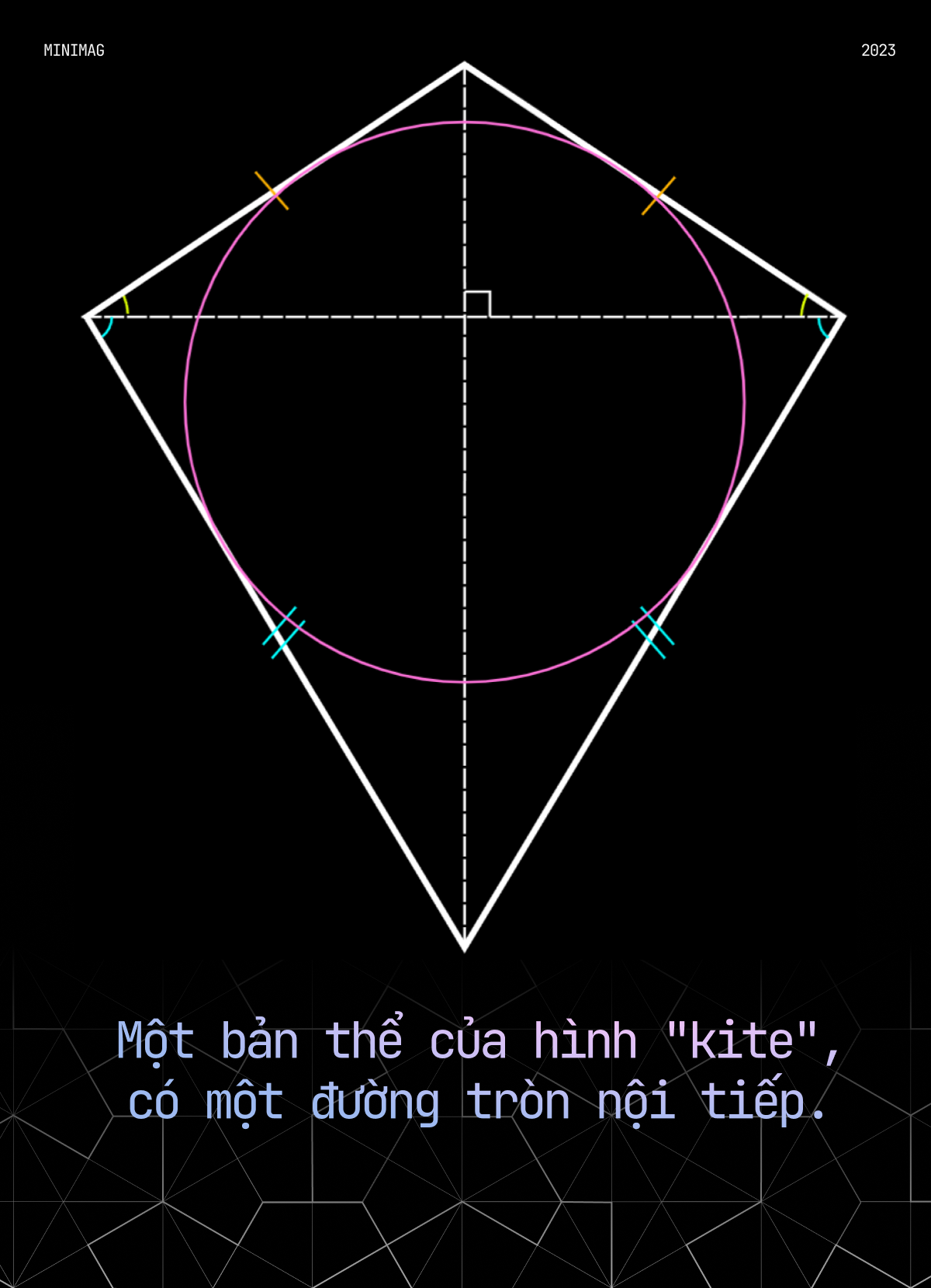
“Khả năng cao có những người khác đã từng mường tượng ra hình hài cái mũ, nhưng không chủ động tìm kiếm khả năng lát mặt phẳng của nó”, Tiến sĩ Kaplan nhận định. “Tôi thích thú với suy nghĩ, rằng hình này lẩn trốn chúng ta giữa thanh thiên bạch nhật”.

Nhận định của nhà toán học công tác tại Đại học Moravian, Doris Schattschneider có thể làm rõ ý của ông Kaplan. “Điều khiến tôi ngạc nhiên nhất là những hình ghép phi chu kỳ này lại đặt vừa vào một lưới lục giác, và hình dáng lưới lục giác thì quá đỗi chu kỳ rồi”, nhà toán học Schattschneider nhận định.

Nhà toán học Marjorie Senechal cũng đồng tình. “Nó nằm ngay giữa những hình lục giác”, bà nói. “Trên thế giới sẽ có bao nhiêu người tự cảm thấy nuối tiếc và tự vấn, tại sao mình lại không nhìn ra hình này nhỉ?”.

Bất ngờ tiếp nối bất ngờ, ông Smith tiếp tục tìm ra một hình einstein nữa. Được đặt tên “con rùa”, hình được ghép không phải từ 8 mà là 10 hình kite. Lập trình viên Myers đưa hình con rùa vào mô hình tính toán và khám phá ra một mối liên hệ sâu sắc giữa cái mũ và con rùa. Ông nhận định có cả một “dòng dõi” các einstein xuất thân từ cái mũ - số lượng nhiều đến bất tận của những hình dáng ghép với nhau theo vô vàn kiểu cách.

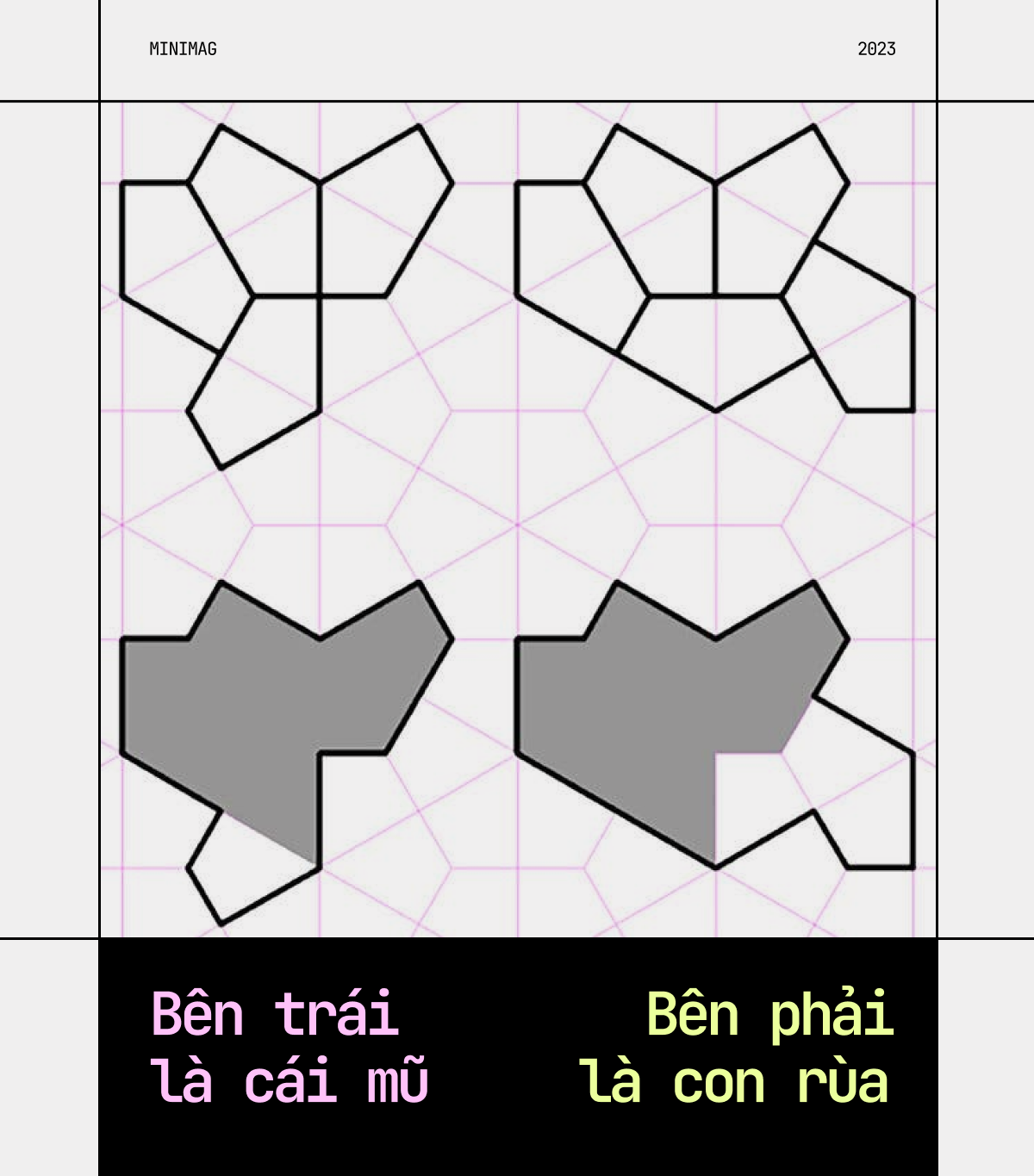
 Ông Smith không mấy hồ hởi trước gia phả khổng lồ xuất thân từ chiếc mũ mà mình tìm ra. “Chúng trông như hàng giả, hay một thứ hình đột biến gì đó”, ông nói.

Dù gì chăng nữa, chính dòng dõi einstein này đã giúp các nhà toán học có thêm một cách thức nữa để chứng minh tính phi chu kỳ. Các phép toán “dường như quá hợp lý để trở thành sự thực”, Tiến sĩ Myers nói. Ông không  hề trông đợi vào việc tìm ra một cách thức mới để chứng minh tính phi chu kỳ, “nhưng có vẻ mọi thứ đều ăn khớp với nhau khi tôi bắt đầu đi sâu vào chi tiết”.

Tính tới thời điểm này, Toán học chưa có nhiều cách chứng minh tính phi chu kỳ. Khi báo cáo khoa học mới được phê duyệt, những người đam mê toán sẽ có một công cụ mới để chơi đùa với những hình dáng và những con số đi kèm.

Nhưng bản thân người tìm ra cái mũ, ông Smith, lại không hứng thú với bài báo cáo nhiều chữ. “Thật tình mà nói, tôi chẳng giúp được gì”. Và ông nói thêm, mừng vì báo cáo khoa học vẫn có hình minh họa: “Tôi là kiểu người thích xem tranh hơn”.

Tham khảo The New York Times, Wired, Science News